|
Herwig++
2.7.0
|
This is the class definition for the UA5Handler. More...
#include <UA5Handler.h>
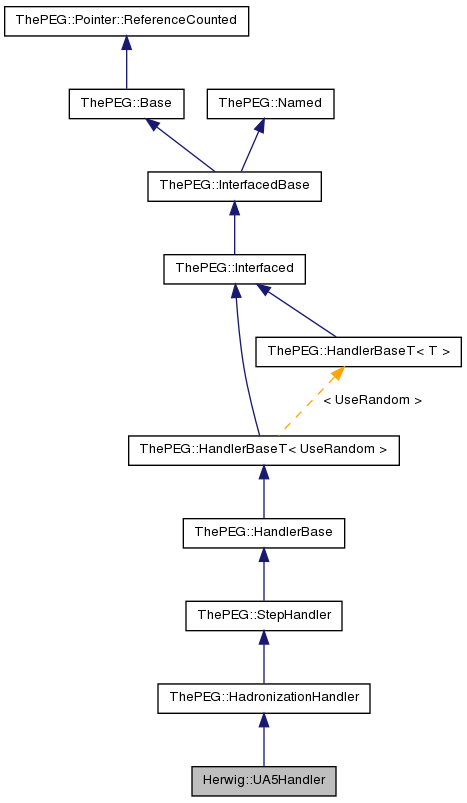
Public Member Functions | |
| virtual void | handle (EventHandler &eh, const tPVector &tagged, const Hint &hint) |
| This is the routine that starts the algorithm. | |
Standard constructors and destructors. | |
| UA5Handler () | |
| The default constructor. | |
Functions used by the persistent I/O system. | |
| void | persistentOutput (PersistentOStream &os) const |
| Function used to write out object persistently. | |
| void | persistentInput (PersistentIStream &is, int version) |
| Function used to read in object persistently. | |
Static Public Member Functions | |
| static void | Init () |
| The standard Init function used to initialize the interfaces. | |
Protected Member Functions | |
Clone Methods. | |
| virtual IBPtr | clone () const |
| Make a simple clone of this object. | |
| virtual IBPtr | fullclone () const |
| Make a clone of this object, possibly modifying the cloned object to make it sane. | |
Private Member Functions | |
| LorentzRotation | rotate (const LorentzMomentum &p) const |
| This returns the rotation matrix needed to rotate p into the z axis. | |
| UA5Handler & | operator= (const UA5Handler &) |
| This is never defined and since it can never be called it isn't needed. | |
| void | performDecay (PPtr parent, int &totalcharge, int &numbercharge) const |
| Members to decay the clusters and hadrons produced in their decay, and insert the output in the event record. | |
| void | decayCluster (ClusterPtr cluster, bool single) const |
| Decay a cluster to two hadrons is sufficiently massive and to one if not. | |
| void | insertParticle (PPtr particle, StepPtr step, bool all) const |
| Recursively add particle and decay products to the step. | |
| double | negativeBinomial (int N, double mean, double ek) const |
| Members to generate the multiplicity according to a negative binomial distribution. | |
| double | meanMultiplicity (Energy E) const |
| The value of the mean multiplicity for a given energy E. | |
| unsigned int | multiplicity (Energy E) const |
| Generates a multiplicity for the energy E according to the negative binomial distribution. | |
| void | generateMomentum (tClusterPtr clu1, tClusterPtr clu2, const ClusterVector &clusters, Energy CME, const Lorentz5Momentum &cm) const |
| Members to generate the momenta of the clusters. | |
| void | generateCylindricalPS (const ClusterVector &clusters, Energy CME) const |
| The implementation of the cylindrical phase space. | |
| template<typename T > | |
| T | gaussDistribution (T mean, T stdev) const |
| Various methods to generate random distributions. | |
| double | randUng (double A, double B) const |
| This returns a random number with a flat distribution [-A,A] plus gaussian tail with stdev B TODO: Should move this to Utilities. | |
| template<typename T > | |
| void | randAzm (T pt, T &px, T &py) const |
| Generates a random azimuthal angle and puts x onto px and py TODO: Should move this to Utilities. | |
| Energy | randExt (Energy AM0, InvEnergy B) const |
This returns random number from 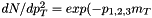 distribution, where distribution, where 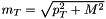 . . | |
Private Attributes | |
| ClusterFissionerPtr | clusterFissioner |
| Reference to the ClusterFissioner object. | |
| ClusterDecayerPtr | clusterDecayer |
| Reference to the cluster decayer object. | |
| double | _probSoft |
| This is the probability of having a soft underlying event. | |
| double | _enhanceCM |
| This is a parameter used to enhance the CM energy used to generate the multiplicity distribution. | |
| unsigned int | _maxtries |
| The maximum number of attempts to generate the distribution. | |
| bool | _needWarning |
| Whether to warn about using UA5 and MPI simultaneously. | |
| double | _n1 |
Parameters for the mean multiplicity 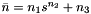 . . | |
| double | _n2 |
The parameter 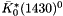 . . | |
| double | _n3 |
The parameter 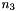 . . | |
| double | _k1 |
Parameters for 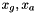 in the negative binomial distribution given by in the negative binomial distribution given by 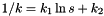 . . | |
| double | _k2 |
The parameter 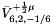 . . | |
| Energy | _m1 |
Parameters for the cluster mass distribution, 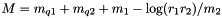 . . | |
| InvEnergy | _m2 |
The parameter 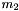 . . | |
| InvEnergy | _p1 |
Parameters for the transverpse momentum of the soft distribution, 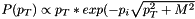 . . | |
| InvEnergy | _p2 |
The parameter 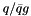 for strange and charm quarks. for strange and charm quarks. | |
| InvEnergy | _p3 |
The parameter  for diquarks. for diquarks. | |
Static Private Attributes | |
| static ClassDescription < UA5Handler > | initUA5Handler |
| The static object used to initialize the description of this class. | |
Detailed Description
This is the class definition for the UA5Handler.
This class is designed to generate an underlying event based on the UA5 model. This is intended as a basic underlying event model which will be superceded by a new model in Herwig++.
This class interfaces with the cluster hadronization. To that end there is an interface set up with the ClusterFissioner class and with the ClusterDecayer class.
The Hadronization is responsible for the formation of the beam clusters. In this step the colour connection between the spectators and the initial-state parton showers is cut by the forced emission of a soft quark-antiquark pair. The underlying soft event in a hard hadron-hadron collision is then assumed to be a soft collision between these two beam clusters.
The model used for the underlying event is based on the minimum-bias 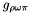 event generator of the UA5 Collaboration, UA5 Collaboration, G.J. Alner et al., Nucl. Phys. B291 (1987) 445, modified to make use of our cluster fragmentation algorithm.
event generator of the UA5 Collaboration, UA5 Collaboration, G.J. Alner et al., Nucl. Phys. B291 (1987) 445, modified to make use of our cluster fragmentation algorithm.
The parameter ProbSoft enables one to produce an underlying event in only a fraction ProbSoft of events (default=1.0).
The UA5 model starts from a parametrization of the 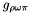 inelastic charged multiplicity distribution as a negative binomial distribution,
inelastic charged multiplicity distribution as a negative binomial distribution,
![\[P(n) = \frac{\Gamma(n+k)}{n!\,\Gamma(k)} \frac{(\bar n/k)^n}{(1+\bar n/k)^{n+k}}\;.\]](form_1476.png)
The parameter 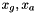 is given by
is given by
![\[1/k =k_1\ln s+k_2,\]](form_1477.png)
and 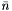 is given by
is given by
![\[\bar n =n_1s^{n_2}+n_3\]](form_1479.png)
As an option, for underlying events the value of 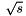 used to choose the multiplicity
used to choose the multiplicity 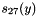 may be increased by a factor EnhanceCM to allow for an enhanced underlying activity in hard events.
may be increased by a factor EnhanceCM to allow for an enhanced underlying activity in hard events.
Once a charged multiplicity has been selected from the above distribution, `softclusters' are generated with flavours 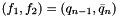 by drawing
by drawing 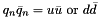 randomly from the vacuum. Soft cluster masses are assigned as
randomly from the vacuum. Soft cluster masses are assigned as
![\[M = m_{q1}+m_{q2}+m_1-\log(r_1 r_2)/m_2 \]](form_1483.png)
where 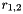 are random numbers, which gives a (shifted) exponential distribution of
are random numbers, which gives a (shifted) exponential distribution of  . The parameters
. The parameters  and
and 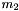 control the distribution and
control the distribution and 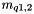 are the masses of the quarks in the cluster.
are the masses of the quarks in the cluster.
As each soft cluster is generated, it is decayed to stable hadrons using the cluster hadronization model (without cluster fission) and the accumulated charged multiplicity is computed. Once the preselected charged multiplicity is exactly reached, cluster generation is stopped. If it is exceeded, all clusters are rejected and new ones are generated until the exact value is reached. In this way the multiplicity distribution of stable charged hadrons is generated exactly as prescribed.
At this stage (to save time) the kinematic distribution of the soft clusters has not yet been generated. The decay products of each cluster are stored in its rest frame. Now the transverse momenta of the clusters are generated with the distribution
![\[P(p_t)\propto p_t\exp\left(-p_{1,2,3}\sqrt{p_t^2+M^2}\right)\]](form_1489.png)
where the slope parameter 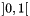 depends as indicated on the flavour of the quark or diquark pair created in the primary cluster decay,
depends as indicated on the flavour of the quark or diquark pair created in the primary cluster decay, 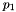 for light quarks,
for light quarks, 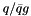 for the strange and charm quarks and
for the strange and charm quarks and  for diquarks. Next the clusters are given a flat rapidity distribution with Gaussian shoulders. The `reduced rapidities'
for diquarks. Next the clusters are given a flat rapidity distribution with Gaussian shoulders. The `reduced rapidities' 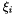 are generated first by drawing from a distribution
are generated first by drawing from a distribution
![\[P(\xi) = N\;\;\;\mbox{for}\;|\xi|<0.6\]](form_1491.png)
![\[P(\xi) = N\,e^{-(\xi-0.6)^2/2} \;\;\;\mbox{for}\;\xi>0.6\]](form_1492.png)
![\[P(\xi) = N\,e^{-(\xi+0.6)^2/2} \;\;\;\mbox{for}\;\xi<-0.6\]](form_1493.png)
where 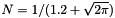 is the normalization. Next a scaling factor
is the normalization. Next a scaling factor 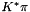 is computed such that the scaled cluster rapidities
is computed such that the scaled cluster rapidities 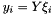 , their masses and transverse momenta satisfy momentum conservation when compared to the total energy of the underlying event. Thus the soft cluster rapidity distribution retains its overall shape but becomes higher and wider as the energy of the underlying event increases.
, their masses and transverse momenta satisfy momentum conservation when compared to the total energy of the underlying event. Thus the soft cluster rapidity distribution retains its overall shape but becomes higher and wider as the energy of the underlying event increases.
Finally the decay products of each cluster are boosted from its rest frame into the lab frame and added to the event record.
- See also:
- The interfaces defined for UA5Handler..
Definition at line 109 of file UA5Handler.h.
Member Function Documentation
| virtual IBPtr Herwig::UA5Handler::clone | ( | ) | const [protected, virtual] |
Make a simple clone of this object.
- Returns:
- a pointer to the new object.
Implements ThePEG::InterfacedBase.
| void Herwig::UA5Handler::decayCluster | ( | ClusterPtr | cluster, |
| bool | single | ||
| ) | const [private] |
Decay a cluster to two hadrons is sufficiently massive and to one if not.
- Parameters:
-
cluster The cluster to decay single Whether or not ot allow decays to
| virtual IBPtr Herwig::UA5Handler::fullclone | ( | ) | const [protected, virtual] |
Make a clone of this object, possibly modifying the cloned object to make it sane.
- Returns:
- a pointer to the new object.
Reimplemented from ThePEG::InterfacedBase.
| T Herwig::UA5Handler::gaussDistribution | ( | T | mean, |
| T | stdev | ||
| ) | const [inline, private] |
Various methods to generate random distributions.
Gaussian distribution
- Parameters:
-
mean the mean of the distribution stdev the standard deviation of the distribution
- Returns:
- Arandom value from the gaussian distribution
| void Herwig::UA5Handler::generateCylindricalPS | ( | const ClusterVector & | clusters, |
| Energy | CME | ||
| ) | const [private] |
The implementation of the cylindrical phase space.
- Parameters:
-
clusters The list of clusters to generate the momentum for CME The center of mass energy
| void Herwig::UA5Handler::generateMomentum | ( | tClusterPtr | clu1, |
| tClusterPtr | clu2, | ||
| const ClusterVector & | clusters, | ||
| Energy | CME, | ||
| const Lorentz5Momentum & | cm | ||
| ) | const [private] |
Members to generate the momenta of the clusters.
This generates the momentum of the produced particles according to the cylindrical phase space algorithm given in Computer Physics Communications 9 (1975) 297-304 by S. Jadach.
- Parameters:
-
clu1 The first incoming cluster clu2 The second incoming cluster clusters The list of clusters produced CME The center of mass energy cm The center of mass momentum (of the underlying event)
| virtual void Herwig::UA5Handler::handle | ( | EventHandler & | eh, |
| const tPVector & | tagged, | ||
| const Hint & | hint | ||
| ) | [virtual] |
This is the routine that starts the algorithm.
- Parameters:
-
eh the EventHandler in charge of the generation. tagged the vector of particles to consider. If empty, all final state particles in the current Step is considered. hint a possible Hint which is ignored in this implementation
Implements ThePEG::StepHandler.
| static void Herwig::UA5Handler::Init | ( | ) | [static] |
The standard Init function used to initialize the interfaces.
Called exactly once for each class by the class description system before the main function starts or when this class is dynamically loaded.
Reimplemented from ThePEG::HadronizationHandler.
| void Herwig::UA5Handler::insertParticle | ( | PPtr | particle, |
| StepPtr | step, | ||
| bool | all | ||
| ) | const [private] |
Recursively add particle and decay products to the step.
- Parameters:
-
particle The particle step The step all Insert this particle as well as children
| double Herwig::UA5Handler::meanMultiplicity | ( | Energy | E | ) | const [inline, private] |
The value of the mean multiplicity for a given energy E.
This is 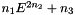 wher
wher 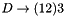 ,
, 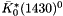 and
and 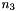 are parameters.
are parameters.
- Parameters:
-
E the energy to calculate the mean multiplicity for
- Returns:
- the mean multiplicity
| unsigned int Herwig::UA5Handler::multiplicity | ( | Energy | E | ) | const [private] |
Generates a multiplicity for the energy E according to the negative binomial distribution.
- Parameters:
-
E The energy to generate for
- Returns:
- the randomly generated multiplicity for the energy given
| double Herwig::UA5Handler::negativeBinomial | ( | int | N, |
| double | mean, | ||
| double | ek | ||
| ) | const [inline, private] |
Members to generate the multiplicity according to a negative binomial distribution.
Calculate the negative binomial probability given the mean 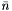 , the multiplicity and
, the multiplicity and 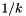 .
.
- Parameters:
-
N The multplicity for which to calculate the probability mean The mean multiplicity 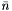
ek 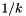
- Returns:
- a value distributed according the negative binomial distribution
| UA5Handler& Herwig::UA5Handler::operator= | ( | const UA5Handler & | ) | [private] |
This is never defined and since it can never be called it isn't needed.
The prototype is defined so the compiler doesn't use the default = operator.
| void Herwig::UA5Handler::performDecay | ( | PPtr | parent, |
| int & | totalcharge, | ||
| int & | numbercharge | ||
| ) | const [private] |
Members to decay the clusters and hadrons produced in their decay, and insert the output in the event record.
Perform the decay of an unstable hadron.
- Parameters:
-
parent the decaying particle totalcharge The totalcharge of the decay proiducts numbercharge The number of stabel charged decay products
| void Herwig::UA5Handler::persistentInput | ( | PersistentIStream & | is, |
| int | version | ||
| ) |
Function used to read in object persistently.
- Parameters:
-
is the persistent input stream read from. version the version number of the object when written.
Reimplemented from ThePEG::Interfaced.
| void Herwig::UA5Handler::persistentOutput | ( | PersistentOStream & | os | ) | const |
Function used to write out object persistently.
- Parameters:
-
os the persistent output stream written to.
Reimplemented from ThePEG::Interfaced.
| void Herwig::UA5Handler::randAzm | ( | T | pt, |
| T & | px, | ||
| T & | py | ||
| ) | const [inline, private] |
Generates a random azimuthal angle and puts x onto px and py TODO: Should move this to Utilities.
- Parameters:
-
pt The magnitude of the transverse momentum px The x component after random rotation py The y component after random rotation
| Energy Herwig::UA5Handler::randExt | ( | Energy | AM0, |
| InvEnergy | B | ||
| ) | const [inline, private] |
This returns random number from 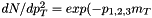 distribution, where
distribution, where 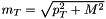 .
.
It uses Newton's method to solve 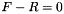
- Parameters:
-
AM0 The mass 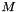 .
. B The slope
- Returns:
- the value distributed from
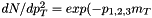 with mean av
with mean av
| double Herwig::UA5Handler::randUng | ( | double | A, |
| double | B | ||
| ) | const [inline, private] |
This returns a random number with a flat distribution [-A,A] plus gaussian tail with stdev B TODO: Should move this to Utilities.
- Parameters:
-
A The width of the flat part B The standard deviation of the gaussian tail
- Returns:
- the randomly generated value
Member Data Documentation
double Herwig::UA5Handler::_k1 [private] |
Parameters for 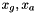 in the negative binomial distribution given by
in the negative binomial distribution given by 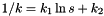 .
.
The parameter 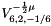
Definition at line 371 of file UA5Handler.h.
Energy Herwig::UA5Handler::_m1 [private] |
Parameters for the cluster mass distribution, 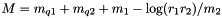 .
.
The parameter 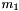
Definition at line 387 of file UA5Handler.h.
double Herwig::UA5Handler::_n1 [private] |
InvEnergy Herwig::UA5Handler::_p1 [private] |
Parameters for the transverpse momentum of the soft distribution, 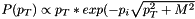 .
.
The parameter 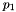 for light quarks
for light quarks
Definition at line 403 of file UA5Handler.h.
ClassDescription<UA5Handler> Herwig::UA5Handler::initUA5Handler [static, private] |
The static object used to initialize the description of this class.
Indicates that this is a concrete class with persistent data.
Definition at line 322 of file UA5Handler.h.
The documentation for this class was generated from the following file:
Generated on Fri Oct 25 2013 10:54:30 for Herwig++ by
 1.7.6.1
1.7.6.1