CMS_2014_I1305624
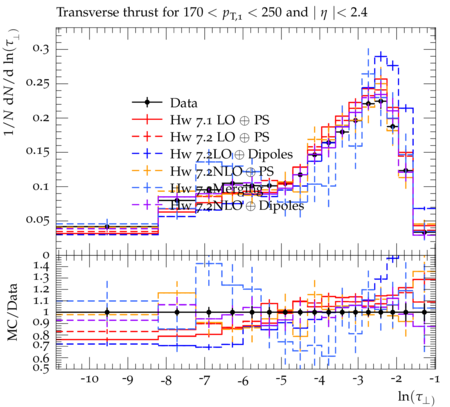
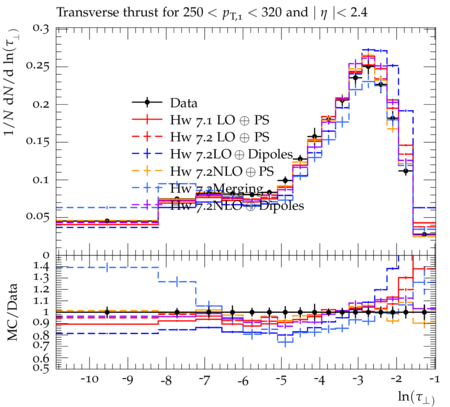
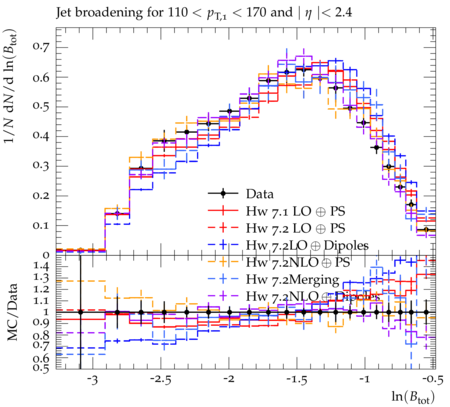
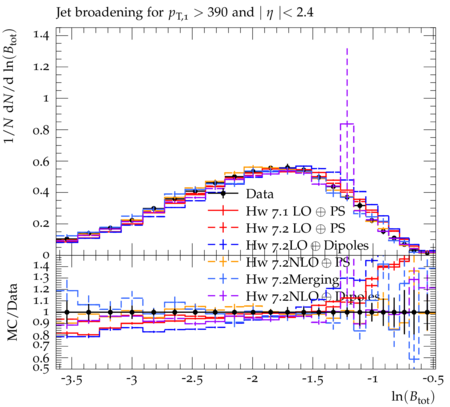
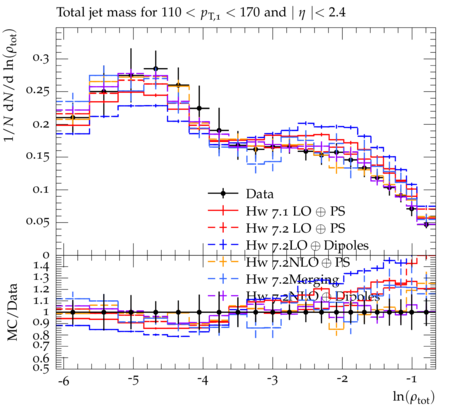
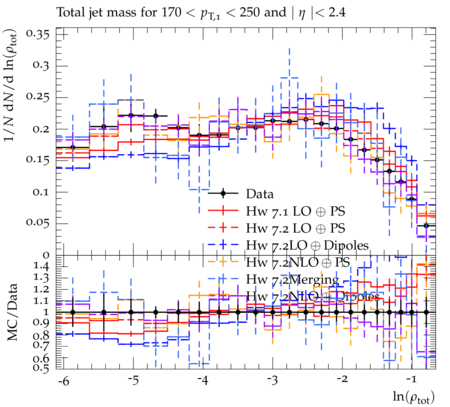
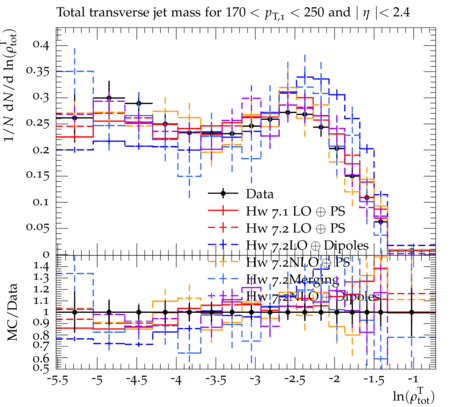
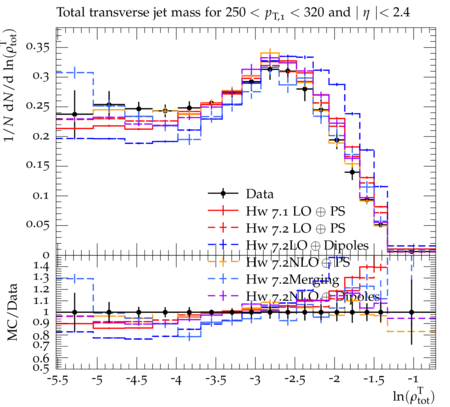
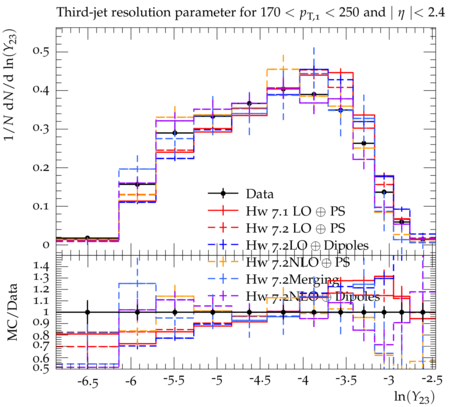
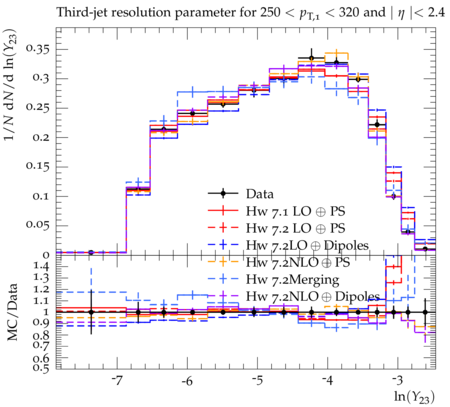
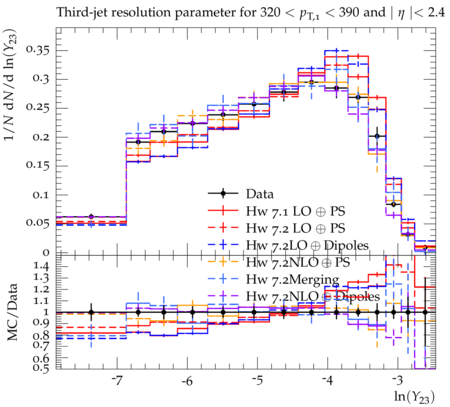
Event-shape variables, which are sensitive to perturbative and nonperturbative aspects of quantum chromodynamic (QCD) interactions, are studied in multijet events recorded in proton-proton collisions at √s=7 TeV. Events are selected with at least one jet with transverse momentum pT>110 GeV and pseudorapidity ∣η∣<2.4, in a data sample corresponding to integrated luminosities of up to 5fb−1. The distributions of five event-shape variables in various leading jet pT ranges are compared to predictions from different QCD Monte Carlo event generators. Five event-shape variables are analyzed in this paper: the transverse thrust τ⊥, the total jet broadening Btot, the total jet mass ρtot, the total transverse jet mass ρTtot and the third-jet resolution parameter Y23. In the formulae below, pT,i, ηi, and ϕi represent the transverse momentum, pseudorapidity, and azimuthal angle of the ith jet, and ˆnT is the unit vector that maximizes the sum of the projections of →pT,i. The transverse thrust axis ˆnT and the beam form the so-called event plane. Based on the direction of ˆnT, the transverse region is separated into an upper side CU, consisting of all jets with →pT⋅ˆnT > 0, and a lower side CL, with →pT⋅ˆnT < 0. The jet broadening and third-jet resolution variables require at least three jets, whereas the calculation of other variables requires at least two jets. The ˆnT vector is defined only up to a global sign - choosing one sign or the other has no consequence since it simply exchanges the upper and lower events regions. Transverse Thrust : The event thrust observable in the transverse plane is defined as τ⊥≡1−max This variable probes the hadronization process and is sensitive to the modeling of two-jet and multijet topologies. In this paper ``multijet' refers to ``more-than-two-jet'. In the limit of a perfectly balanced two-jet event, \tau_{\perp} is zero, while in isotropic multijet events it amounts to (1-2/\pi). Jet Broadenings : The pseudorapidities and the azimuthal angles of the axes for the upper and lower event regions are defined by \begin{eqnarray} \eta_X & \equiv & \frac{\sum_{i\in{\cal{C}}_X} p_{T,i}\eta_i}{\sum_{i\in{\cal{C}}_X} p_{T,i}} , \\ \phi_X & \equiv & \frac{\sum_{i\in{\cal{C}}_X} p_{T,i}\phi_i}{\sum_{i\in{\cal{C}}_X} p_{T,i}} , \end{eqnarray} where X refers to upper (U) or lower (L) side. From these, the jet broadening variable in each region is defined as \begin{eqnarray} B_{X} & \equiv & \frac{1}{2P_{T}} \sum_{i\in{\cal{C}}_X}p_{T,i}\sqrt{(\eta_i -\eta_X)^2 + (\phi_i - \phi_X)^2} , \end{eqnarray} where P_{T} is the scalar sum of the transverse momenta of all the jets. The total jet broadening is then defined as \begin{eqnarray} B_{tot} & \equiv & B_{U} + B_{L}. \end{eqnarray} Jet Masses : The normalized squared invariant mass of the jets in the upper and lower regions of the event is defined by \begin{eqnarray} \rho_X & \equiv & \frac{M^2_X}{P^2}, \end{eqnarray} where M_X is the invariant mass of the constituents of the jets in the region X, and P is the scalar sum of the momenta of all constituents in both sides. The jet mass variable is defined as the sum of the masses in the upper and lower regions, \begin{eqnarray} \rho_{tot} & \equiv & \rho_U + \rho_L . \end{eqnarray} The corresponding jet mass in the transverse plane, \rho^T_{tot}, is also similarly calculated in transverse plane. Third-jet resolution parameter : The third-jet resolution parameter is defined as \begin{eqnarray} Y_{23} \equiv \frac{\mathrm{min}(p_{T,3}^2,[\mathrm{min}(p_{T,i}, p_{T,j})^2 \times (\Delta R_{ij})^2/R^2])}{P_{12}^2} , \end{eqnarray} where i, j run over all three jets, (\Delta R_{ij})^2 = (\eta_i - \eta_j)^2 + (\phi_i - \phi_j)^2, and p_{T,3} is the transverse momentum of the third jet in the event. If there are more than three jets in the event, they are iteratively merged using the k_T algorithm with a distance parameter R = 0.6. To compute P_{12}, three jets are merged into two using the procedure described above and P_{12} is then defined as the scalar sum of the transverse momenta of the two remaining jets. The Y_{23} variable estimates the relative strength of the p_T of the third jet with respect to the other two jets. It vanishes for two-jet events, and a nonzero value of Y_{23} indicates the presence of hard parton emission, which tests the parton showering model of QCD event generators. A test like this is less sensitive to the details of the underlying event (UE) and parton hadronization models than the other event-shape variables.
Generated at Thursday, 12. December 2019 02:35PM