CMS_2016_I1413748
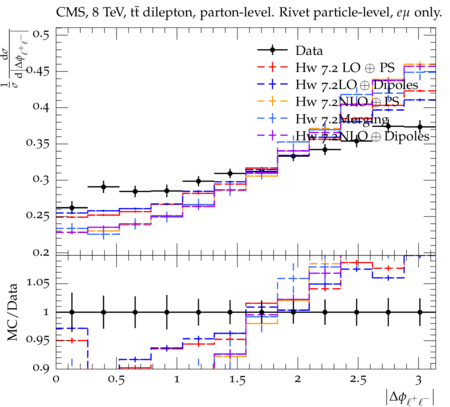
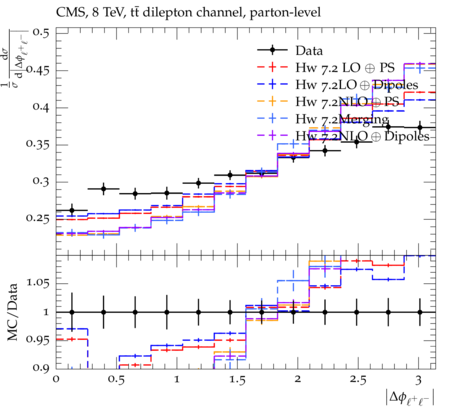
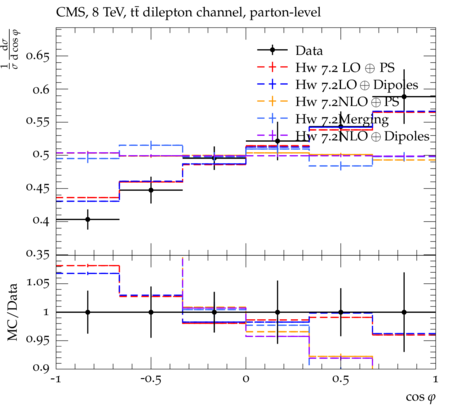
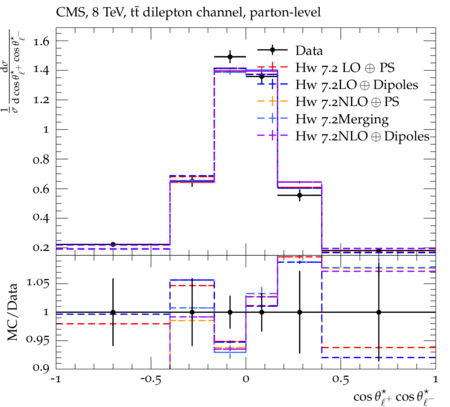
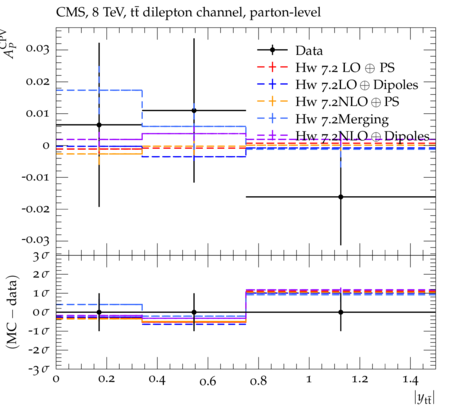
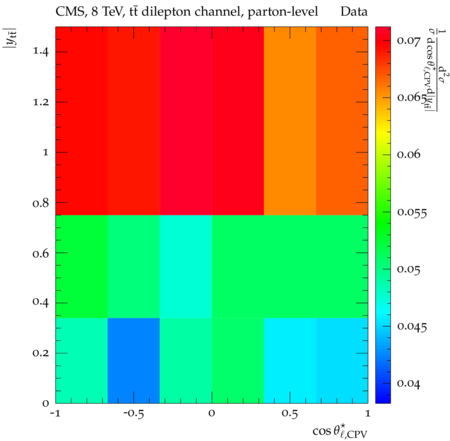
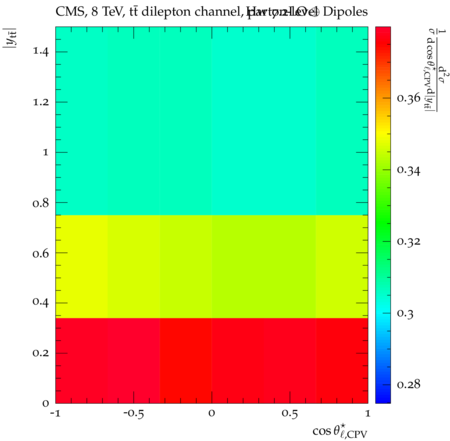
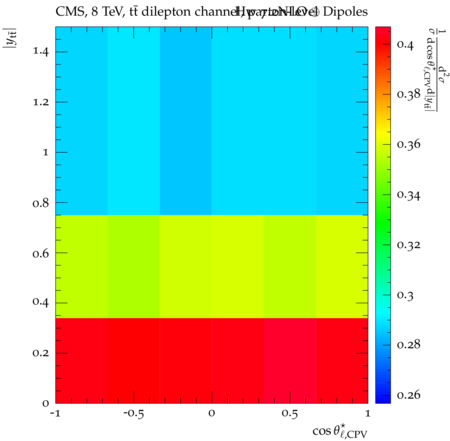
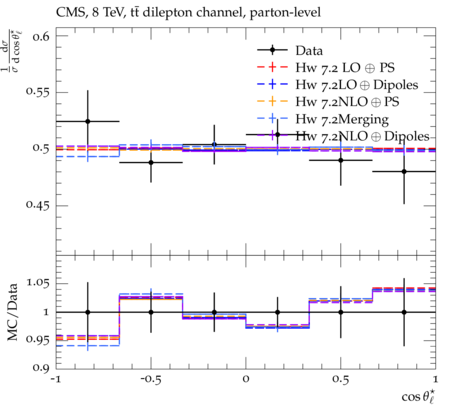
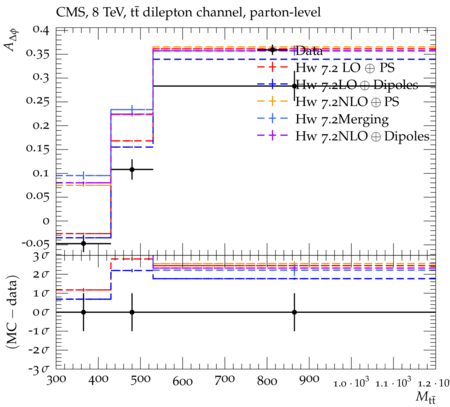
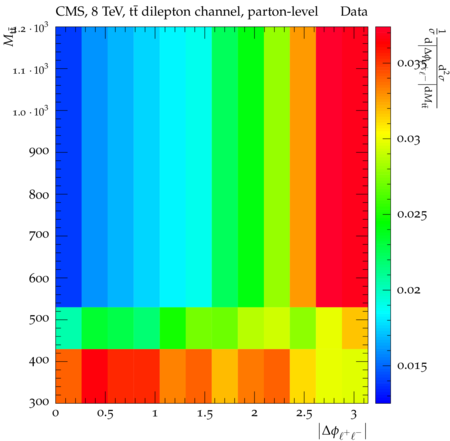
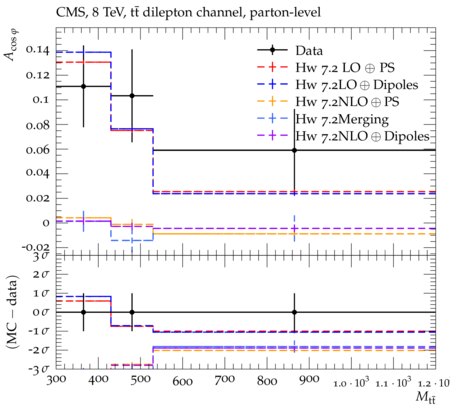
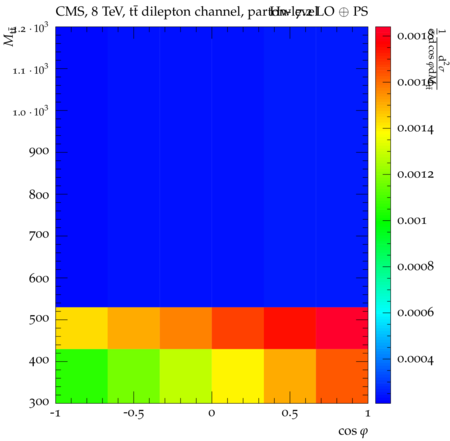
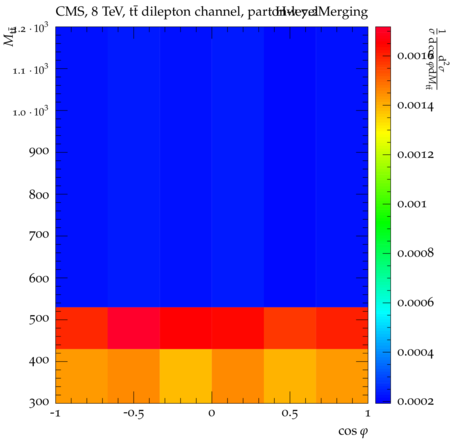
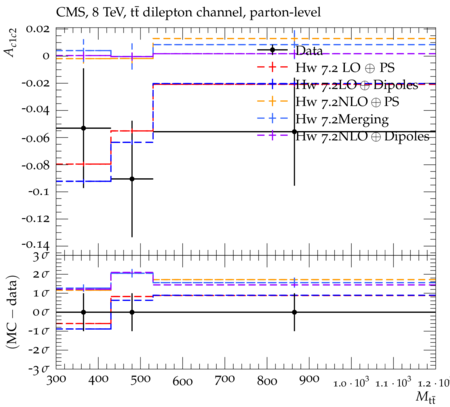
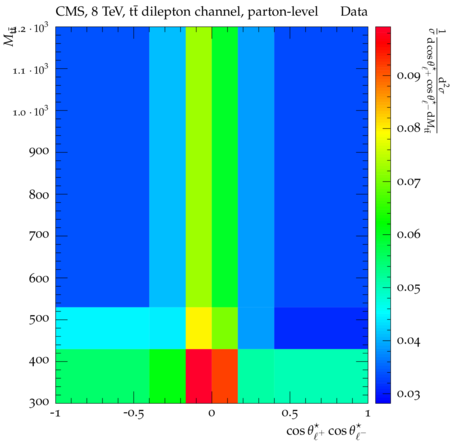
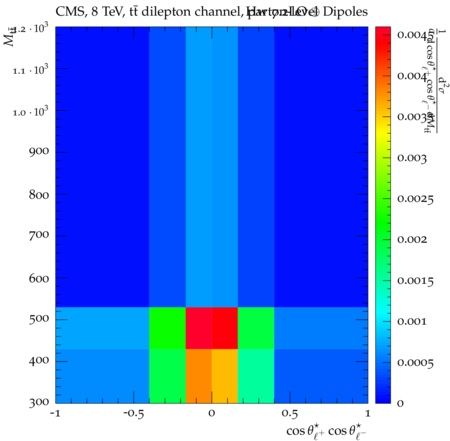
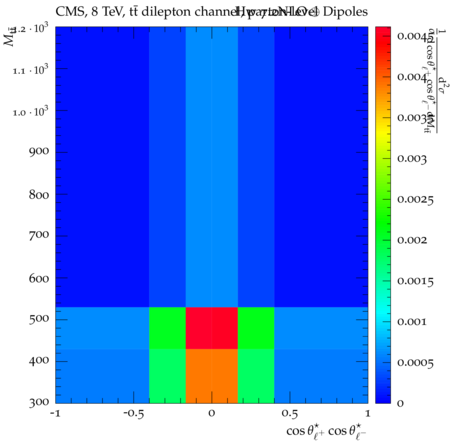
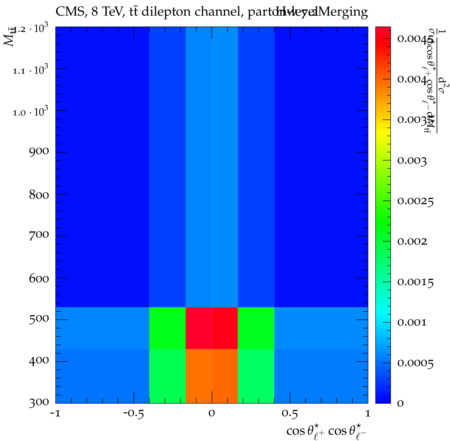
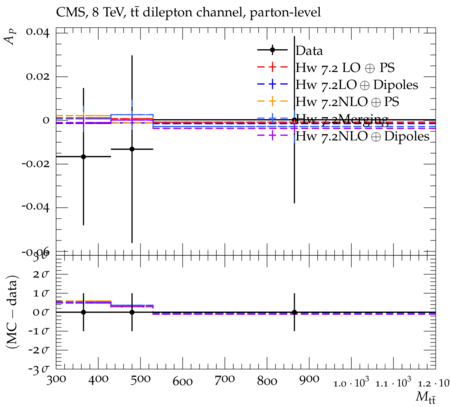
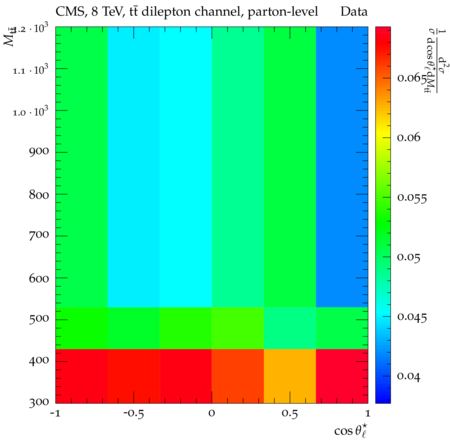
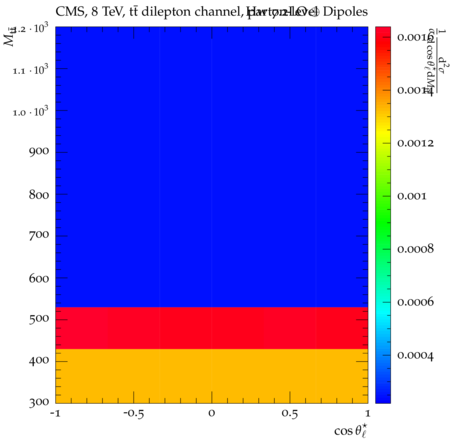
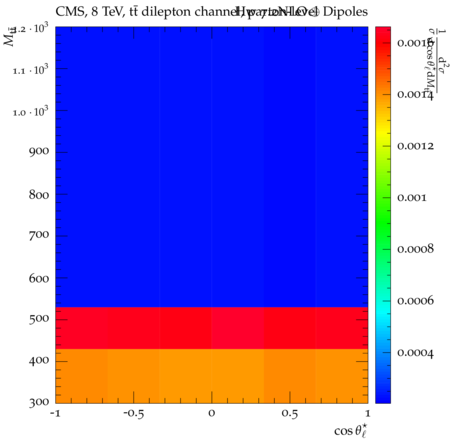
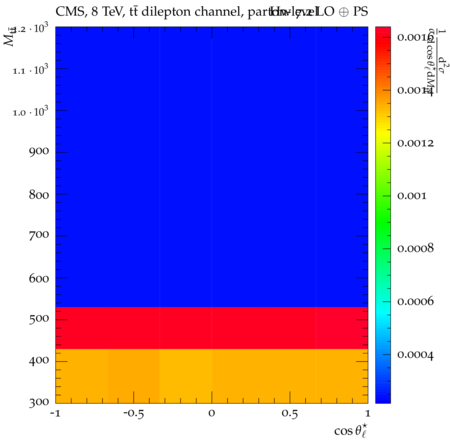
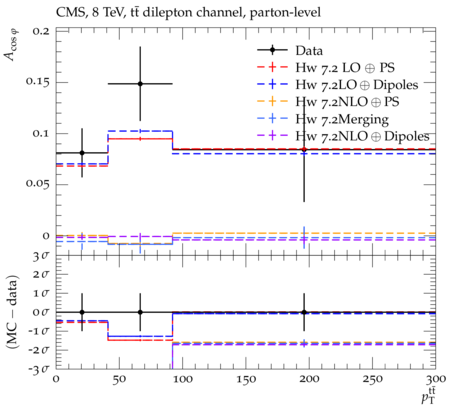
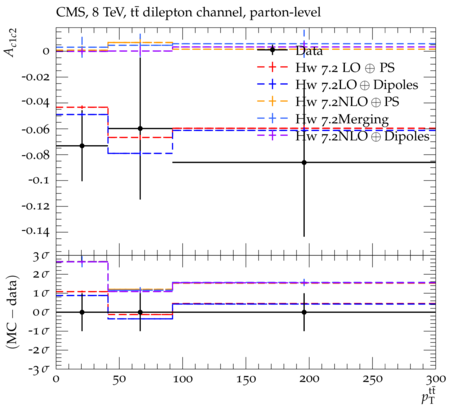
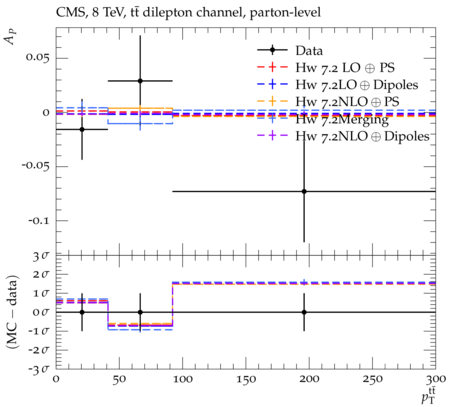
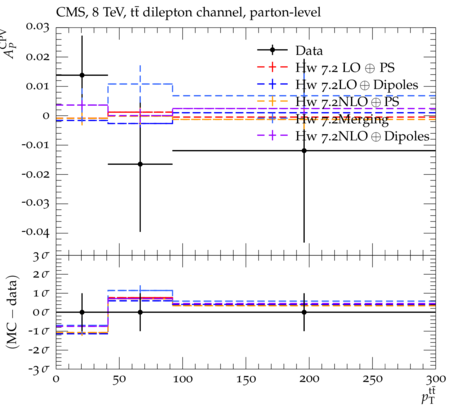
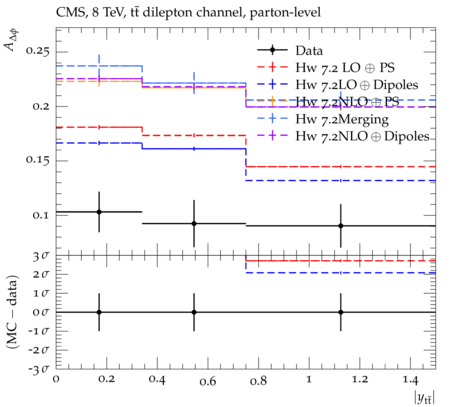
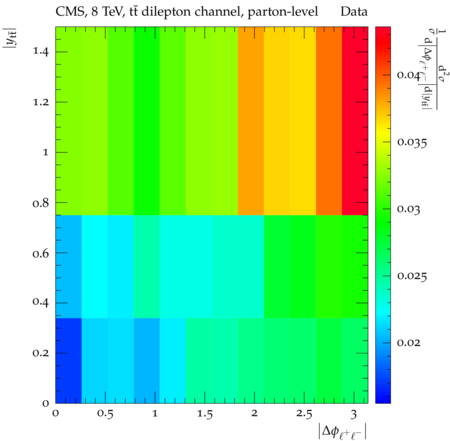
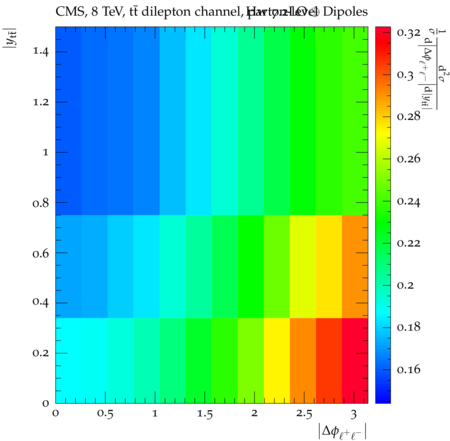
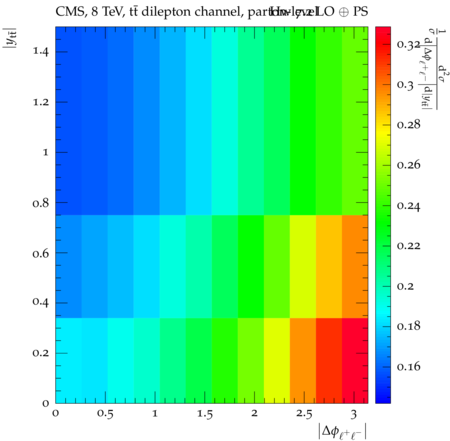
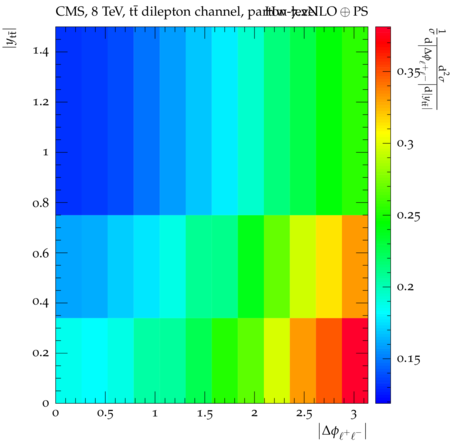
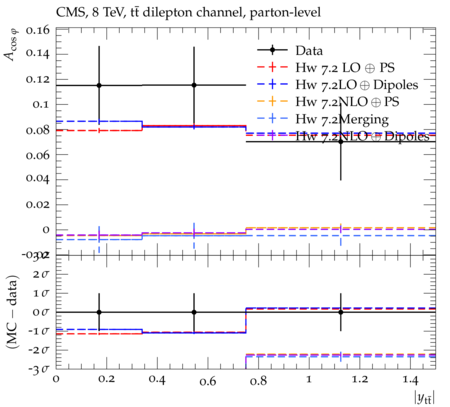
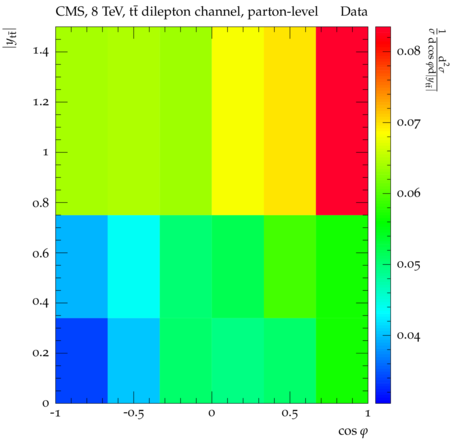
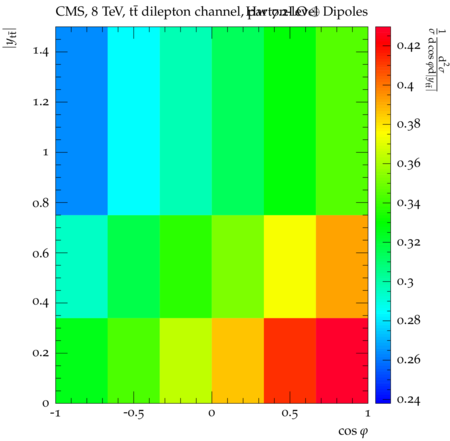
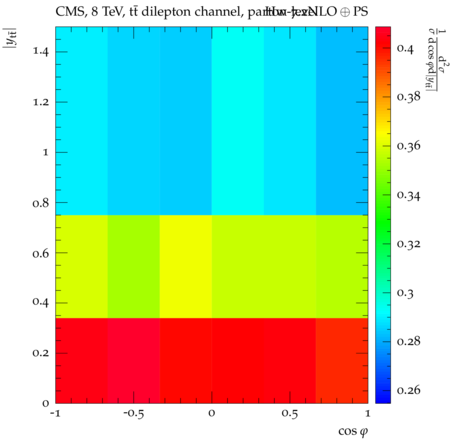
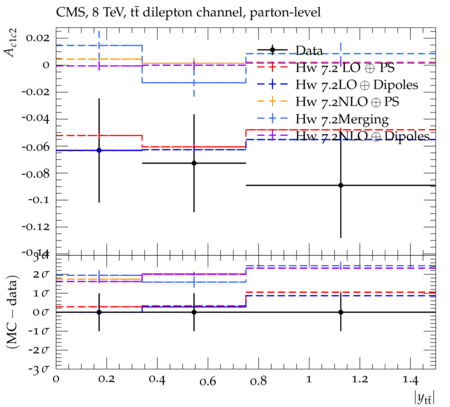
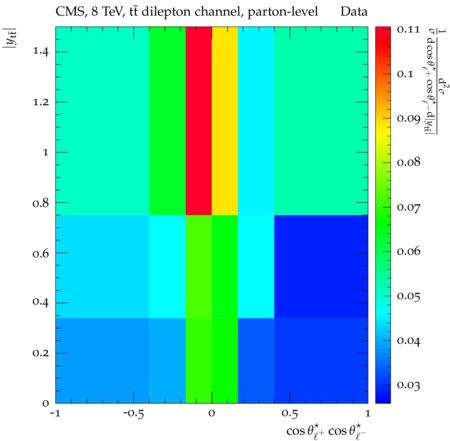
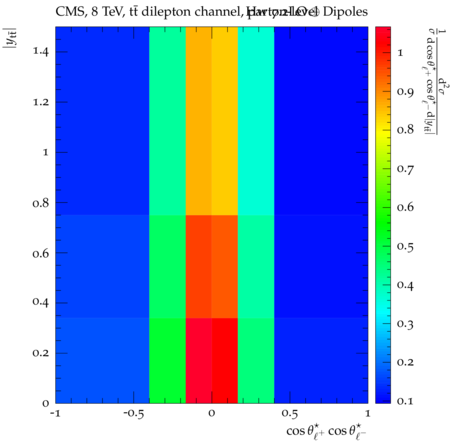
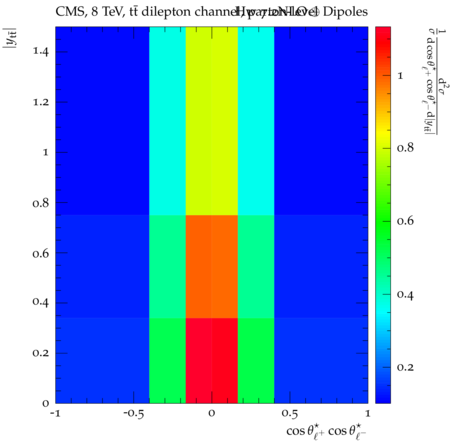
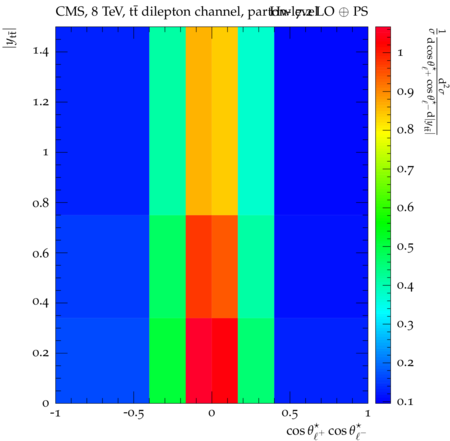
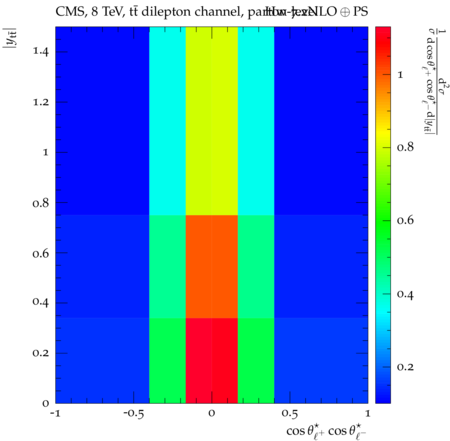
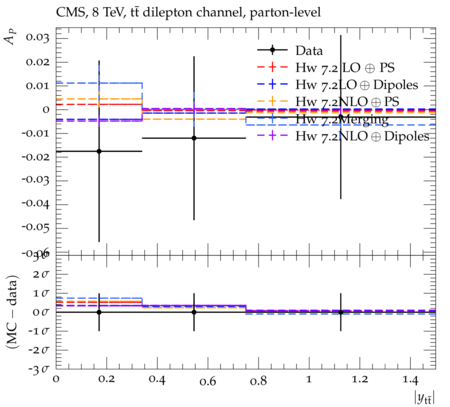
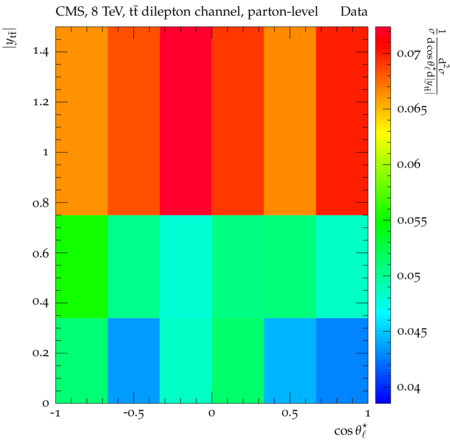
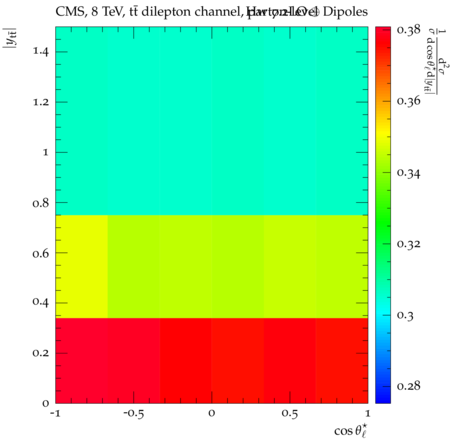
Abstract: Measurements of the top quark-antiquark (tˉt) spin correlations and the top quark polarization are presented for tˉt pairs produced in pp collisions at √s=8TeV. The data correspond to an integrated luminosity of 19.5 fb−1 collected with the CMS detector at the LHC. The measurements are performed using events with two oppositely charged leptons (electrons or muons) and two or more jets, where at least one of the jets is identified as originating from a bottom quark. The spin correlations and polarization are measured from the angular distributions of the two selected leptons, both inclusively and differentially, with respect to the invariant mass, rapidity, and transverse momentum of the tˉt system. The measurements are unfolded to the parton level and found to be in agreement with predictions of the standard model. A search for new physics in the form of anomalous top quark chromo moments is performed. No evidence of new physics is observed, and exclusion limits on the real part of the chromo-magnetic dipole moment and the imaginary part of the chromo-electric dipole moment are evaluated. Particle-level addition to Rivet routine: While the analysis was performed at the parton-level only, |Δϕℓ+ℓ−| is a purely leptonic variable and it has been checked that the results of the analysis would have been essentially unchanged had it been defined at particle-level using dressed leptons instead of using the parton-level top quark daughter leptons. We therefore include both particle- and parton-level versions of this distribution in the Rivet routine, with the former identified in the plot title. For same-flavour dilepton final states, the particle-level definition in the full phase space is problematic because the two leptons can come from fully-hadronic tˉt plus a dilepton pair from radiation. Such pairs have invariant mass Mℓℓ∼0 and produce a peak near zero in the |Δϕℓ+ℓ−| distribution. We therefore select only the tˉt→eμ final state, by requiring exactly one electron and exactly one muon. Note this means tˉt→eμ events with additional dilepton pairs from radiation are vetoed. For PYTHIA8 this amounts to 0.5% of tˉt→eμ events - well below the level of sensitivity of the measured distribution. Histograms and covariance matrices: The error bars in the measured distributions should not be used for fitting because there are significant correlations between bins. The covariance matrices for the statistical and systematic uncertainties in each distribution can be found in hepdata. The single-differential cross sections in hepdata are normalised to unit area (i.e. the integral is equal to one), while the double-differential cross sections in hepdata are normalised to the sum of entries (such that the sum of all bin heights is equal to one). This should be taken into account when comparing the measured distributions to the Rivet results and when using the covariance matrices. Overflow bins: The upper Mtˉt, ptˉtT, and |ytˉt| bins contain overflow events up to infinity.
Generated at Thursday, 12. December 2019 02:35PM